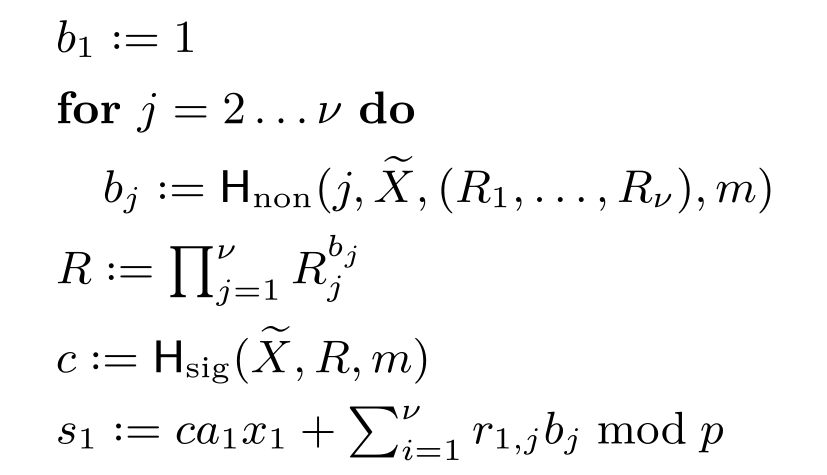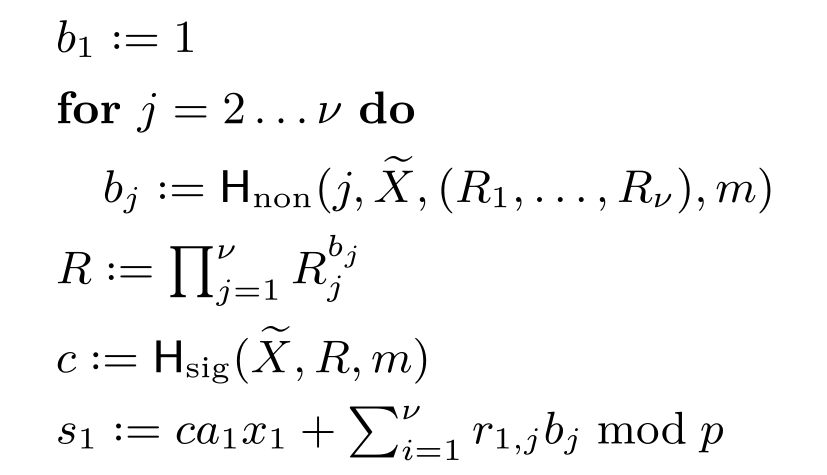
Abstract: Multi-signatures enable a group of signers to produce a single signature on a given message. Recently, Drijvers et al. (S&P’19) showed that all thus far proposed two-round multi-signature schemes in the DL setting (without pairings) are insecure under concurrent sessions, i.e., if a single signer participates in multiple signing sessions concurrently. While Drijvers et al. improve the situation by constructing a secure two-round scheme, saving a round comes with the price of having less compact signatures. In particular, the signatures produced by their scheme are more than twice as large as Schnorr signatures, which arguably are the most natural and compact among all practical DL signatures and are therefore becoming popular in cryptographic applications (e.g., support for Schnorr signature verification has been proposed to be included in Bitcoin). If one needs a multi-signature scheme that can be used as a drop-in replacement for Schnorr signatures, then one is either forced to resort to a three-round scheme such as MuSig (Maxwell et al., DCC 2019) or MSDL-pop (Boneh, Drijvers, and Neven, ASIACRYPT 2018), or to accept that signing sessions are only secure when run sequentially, which may be hard to enforce in practice, e.g., when the same signing key is used by multiple devices.
In this work, we propose MuSig2, a novel and simple two-round multi-signature scheme variant of the MuSig scheme. Our scheme is the first multi-signature scheme that simultaneously i) is secure under concurrent signing sessions, ii) supports key aggregation, iii) outputs ordinary Schnorr signatures, iv) needs only two communication rounds, and v) has similar signer complexity as regular Schnorr signatures. Furthermore, our scheme is the first multi-signature scheme in the DL setting that supports preprocessing of all but one rounds, effectively enabling a non-interactive signing process, without forgoing security under concurrent sessions. The combination of all these features makes MuSig2 highly practical. We prove the security of MuSig2 under the one-more discrete logarithm (OMDL) assumption in the random oracle model, and the security of a more efficient variant in the combination of the random oracle and algebraic group models.
Read more on the Blockstream Blog.